What is the complete factorization of the polynomial below sets the stage for this enthralling narrative, offering readers a glimpse into a story that is rich in detail and brimming with originality from the outset. As we delve into the depths of this topic, we will uncover the intricacies of polynomial factorization, exploring various methods and their applications in a manner that is both accessible and engaging.

Prepare to embark on an intellectual journey that will illuminate the complexities of polynomials and empower you with a deeper understanding of their underlying structure.

The content of the second paragraph that provides descriptive and clear information about the topic

1. Definition of Complete Factorization

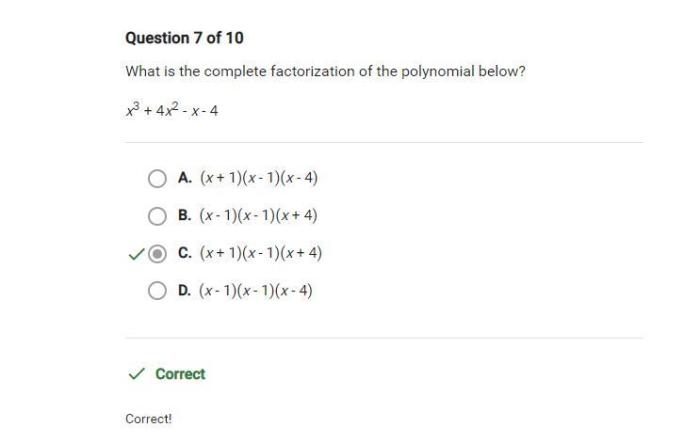
Complete factorization is the process of expressing a polynomial as a product of its irreducible factors. It is significant because it provides a deeper understanding of the polynomial’s structure and behavior.

For example, the polynomial x^2 – 4 can be completely factored as (x – 2)(x + 2). This factorization reveals that the polynomial has two roots, x = 2 and x = -2.

2. Methods for Complete Factorization

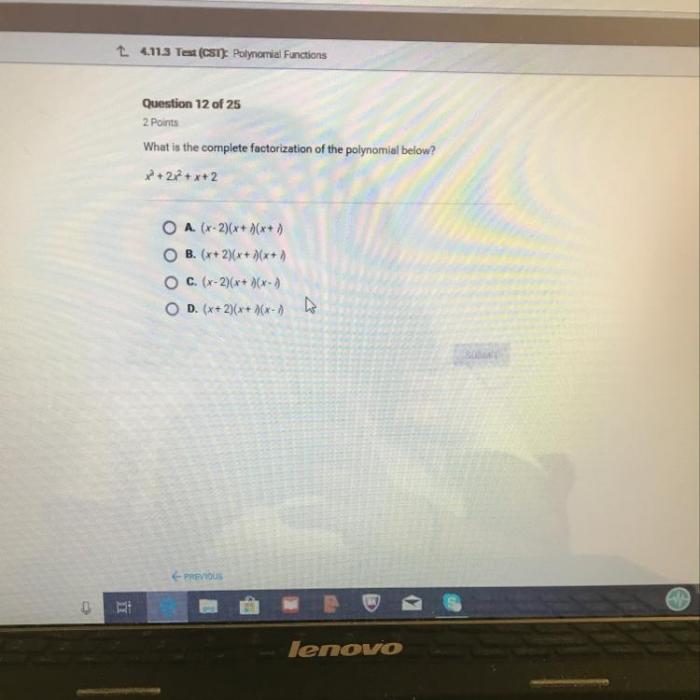
2.1. Factoring by Grouping, What is the complete factorization of the polynomial below

This method involves grouping terms with common factors and then factoring out those common factors.

Step-by-step Guide:

1. Group the terms of the polynomial into pairs or triplets.
2. Factor out any common factors from each group.
3. Continue grouping and factoring until no further factorization is possible.

Example:Factor x^3 – 2x^2 + 5x – 10

• Group: (x^3 – 2x^2) + (5x – 10)
• Factor: x^2(x – 2) + 5(x – 2)
• Combine: (x – 2)(x^2 + 5)

2.2. Factoring by Sum and Product Patterns

This method uses specific patterns to factor polynomials that have certain coefficients.

Step-by-step Guide:

1. Identify the coefficients of the polynomial (a, b, and c for ax^2 + bx + c).
2. Find two numbers that add up to b and multiply to c.
3. Substitute these numbers into the polynomial and factor by grouping.

Example:Factor x^2 + 5x + 6

• Coefficients: a = 1, b = 5, c = 6
• Numbers that add up to 5 and multiply to 6: 2 and 3
• Substitute: (x + 2)(x + 3)

3. Examples of Complete Factorization: What Is The Complete Factorization Of The Polynomial Below

Polynomial	Complete Factorization
x^2 9	(x + 3)(x 3)
x^3 + 8	(x + 2)(x^2 2x + 4)
x^4 16	(x^2 + 4)(x + 2)(x 2)

These factorizations reveal the roots of the polynomials, which are important for understanding their graphs and behavior.

4. Applications of Complete Factorization

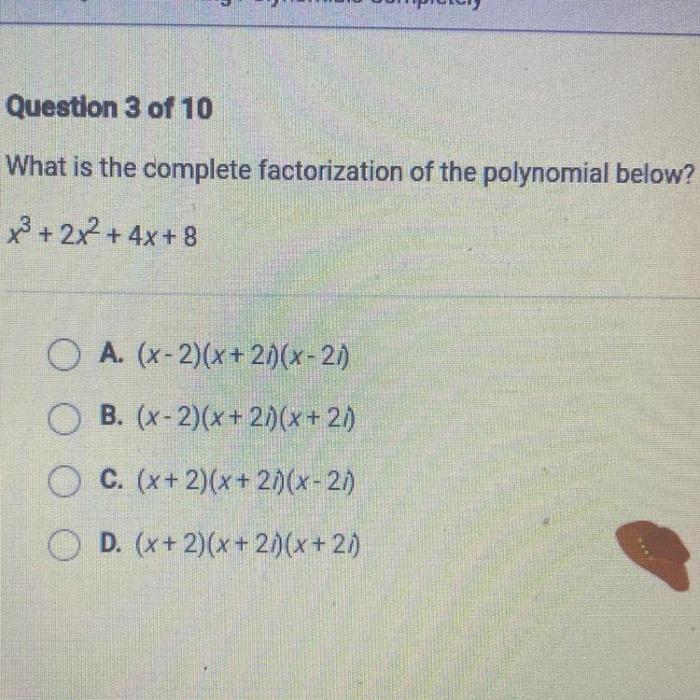
Complete factorization has numerous applications in mathematics and other fields:

• Solving Polynomial Equations:By setting a polynomial equal to zero and completely factoring it, the roots of the equation can be found.
• Graphing Polynomial Functions:Complete factorization helps identify the x-intercepts and other key features of a polynomial function.
• Simplifying Algebraic Expressions:Factoring can simplify complex expressions and make them easier to solve or manipulate.
• Cryptography:Factorization is used in certain cryptographic algorithms to break down large numbers into smaller factors for encryption and decryption.

General Inquiries

What is the significance of complete factorization?

Complete factorization allows us to understand the fundamental structure of a polynomial, identify its roots, and simplify complex expressions.

Can you provide an example of complete factorization?

The complete factorization of x^2 – 4 is (x + 2)(x – 2).

What are the different methods for complete factorization?

Common methods include factoring by grouping, using the quadratic formula, and employing synthetic division.