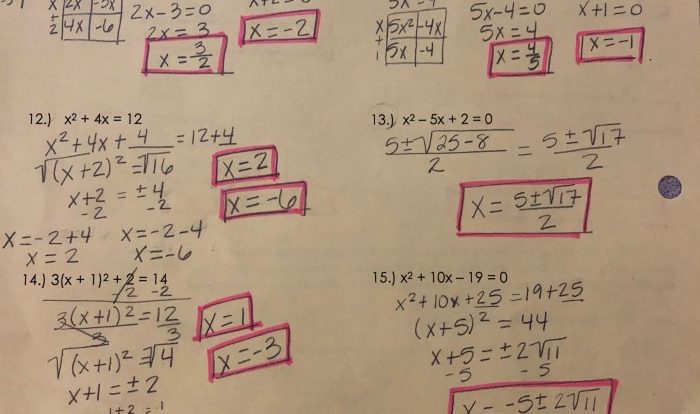Select the polynomial that is a perfect square trinomial. – Delving into the realm of polynomials, this guide presents a comprehensive exploration of perfect square trinomials. Beginning with an introduction to the fundamental concepts of polynomials and trinomials, we delve into the defining characteristics of perfect square trinomials, equipping you with the knowledge to confidently identify and factor these expressions.
As we progress, we will unravel the intricacies of identifying perfect square trinomials, utilizing a step-by-step method and exploring the significance of the discriminant in determining their nature. Moreover, we will delve into the practical applications of perfect square trinomials in solving equations and simplifying expressions.
1. Polynomial Basics
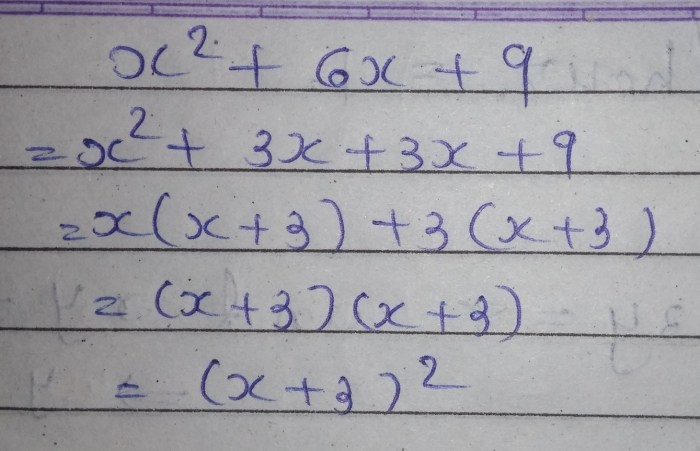
A polynomial is an algebraic expression that consists of constants and variables, combined using addition, subtraction, and multiplication. A trinomial is a polynomial with three terms, usually in the form of ax² + bx + c, where a, b, and c are constants.
A perfect square trinomial is a trinomial that can be expressed as the square of a binomial, or (a + b)². Its structure is a² + 2ab + b².
2. Identifying Perfect Square Trinomials
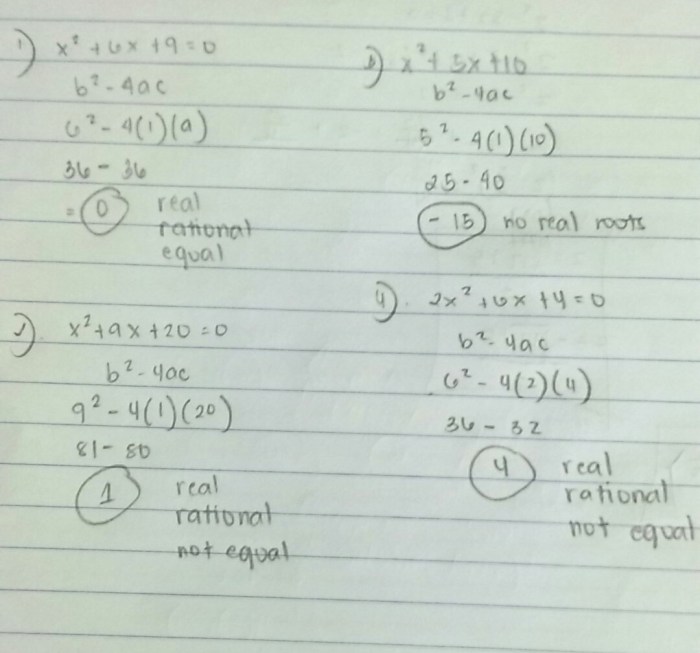
To identify a perfect square trinomial, follow these steps:
- Check if the first and last terms are perfect squares.
- Check if the middle term is twice the product of the square roots of the first and last terms.
If both conditions are met, the trinomial is a perfect square trinomial.
| Trinomial | Factors |
|---|---|
| x² + 4x + 4 | (x + 2)² |
4x²
|
(2x
|
The discriminant of a trinomial, b² – 4ac, determines its nature. If the discriminant is positive, the trinomial is a perfect square trinomial.
3. Factoring Perfect Square Trinomials

To factor a perfect square trinomial, use the formula:
(a + b)² = a² + 2ab + b²
For example, to factor x² + 4x + 4:
- Identify a as x and b as 2.
- Substitute the values into the formula: (x + 2)².
4. Applications of Perfect Square Trinomials: Select The Polynomial That Is A Perfect Square Trinomial.
Perfect square trinomials have various applications, including:
- Solving equations by completing the square.
- Simplifying expressions by factoring out perfect squares.
- Finding the area of squares and rectangles.
- Solving quadratic equations by using the quadratic formula.
In real-world scenarios, perfect square trinomials are encountered in:
- Physics: calculating the trajectory of projectiles.
- Engineering: designing bridges and buildings.
- Finance: modeling investment returns.
Question Bank
What is the key characteristic of a perfect square trinomial?
A perfect square trinomial is a trinomial that can be expressed as the square of a binomial.
How can I identify a perfect square trinomial?
You can identify a perfect square trinomial by checking if the first and last terms are perfect squares and if the middle term is twice the product of the square roots of the first and last terms.
What is the discriminant of a trinomial?
The discriminant of a trinomial is a value that determines the nature of the trinomial. A discriminant of 0 indicates a perfect square trinomial, a discriminant of less than 0 indicates a trinomial with no real roots, and a discriminant of greater than 0 indicates a trinomial with two distinct real roots.