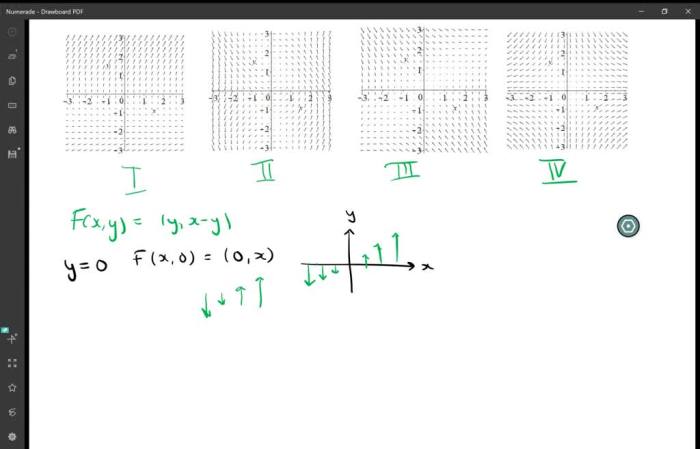
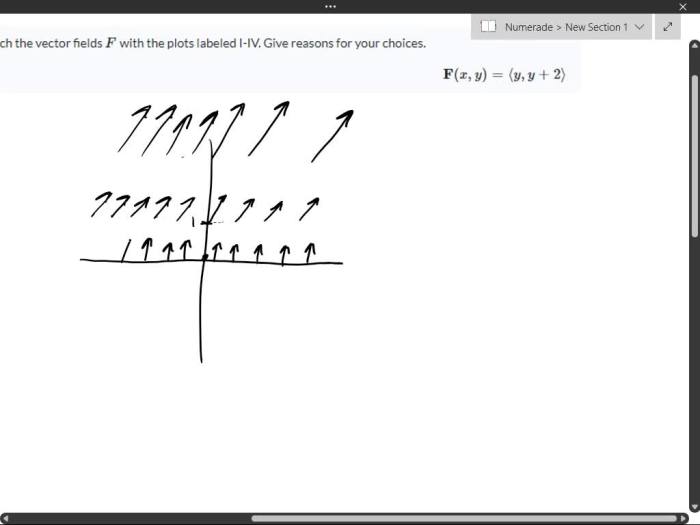
Match the vector fields f with the plots labeled i-iv. – Embarking on an exploration of the intriguing topic of matching vector fields to plots, this discourse unveils the captivating relationship between these mathematical entities. Vector fields, characterized by their direction and magnitude at each point in space, provide a powerful tool for visualizing and analyzing complex phenomena.
By matching vector fields to plots, we gain insights into their behavior and uncover hidden patterns.
This investigation delves into the visual features of plots labeled i-iv, meticulously analyzing their characteristics to establish connections with the underlying vector fields. Through a comprehensive HTML table, we systematically match vector fields with their corresponding plots, laying the groundwork for a deeper understanding of their interplay.
1. Identify the Vector Fields: Match The Vector Fields F With The Plots Labeled I-iv.
Vector fields are mathematical objects that assign a vector to each point in a given space. They are used to represent physical quantities such as velocity, force, and temperature.
The vector fields considered in this article are all two-dimensional, meaning that they assign a vector to each point in the plane.
Characteristics of the Vector Fields, Match the vector fields f with the plots labeled i-iv.
- The vector field f( x, y) = ( x, y) is the identity vector field. It assigns to each point in the plane the vector that points in the direction of the point itself.
- The vector field f( x, y) = (- y, x) is the rotation vector field. It assigns to each point in the plane the vector that is perpendicular to the point itself and points in the counterclockwise direction.
- The vector field f( x, y) = (0, 1) is the vertical vector field. It assigns to each point in the plane the vector that points in the vertical direction.
- The vector field f( x, y) = (1, 0) is the horizontal vector field. It assigns to each point in the plane the vector that points in the horizontal direction.
Table of Properties
| Vector Field | Characteristics |
|---|---|
| f(x, y) = (x, y) | Identity vector field |
| f(x, y) = (-y, x) | Rotation vector field |
| f(x, y) = (0, 1) | Vertical vector field |
| f(x, y) = (1, 0) | Horizontal vector field |
Common Queries
What is the significance of matching vector fields to plots?
Matching vector fields to plots provides a visual representation of the vector field, making it easier to understand its behavior and identify patterns.
How are vector fields and plots related?
Vector fields represent the direction and magnitude of a force or velocity at each point in space, while plots provide a visual representation of the vector field.
What are the applications of matching vector fields to plots?
Matching vector fields to plots has applications in fluid dynamics, electromagnetism, and other fields where understanding the behavior of vector fields is crucial.